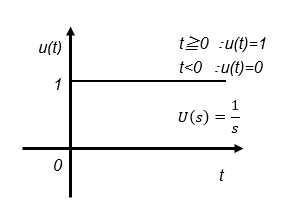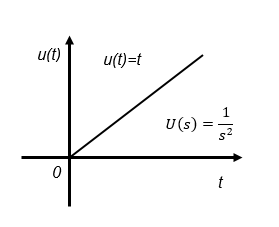マイコンで実現するフィードバック制御のための基礎知識【準備編】
組み込み・マイコンを使ったモーションコントロールを実現するうえで使いこなせれば設計開発の世界が広がる制御理論の概要について自分なりにまとめてみました。制御といってもプログラミングのように命令順に実行するシーケンス制御ではなく、コントロール対象の出力を入力側に返して比較修正するフィードバック制御についてです 。
一般的に制御工学と呼ばれている分野のもので、市販の書物や教科書などに書かれている内容は物理的なものというよりむしろ数学的で初心者には抽象的すぎて独学ではとても簡単に理解できるものではありません。そこで、できるだけ数学的なものが物理的には何を意味するかを意識してポイントを絞ってまとめてみました。
当サイトではフィードバック制御は今後紹介するモーションコントロールで扱うために、具体的にDCモータやその周辺の電気回路などを取り上げていますので、概要をつかんでほしいと思います。ある程度理解ができるようになれば、さらに踏み込んで内容の知識を広げるために、インターネット上でさまざまな人がいろいろな表現解説しているものを参考にして別の角度からみるとさらに本質の理解が深まると思います。
準備編では制御対象をDCモータの回路方程式や運動方程式によるモデリングするところまでを解説します。解析編ではモデリングした制御対象にフィードバック情報を適切に与える時のポイントについて解説します。応用編ではPID制御や、DCモータの速度制御など実際に現場で使われている技術について解説します。
目次
フィードバック制御とは…一般なシーケンス制御との違い

一般的に自動制御といえば大きく分けてシーケンス制御とフィードバック制御に分類されます。 シーケンス制御とはリレー回路などで組み合わせた工程やプログラミングした工程で設定した条件のとおりに機能するもので オープンループ制御、開ループ制御とも呼ばれます。


産業機械を制御するPLC(Programmable Logic Controller)は典型的なシーケンス制御です。身近な例では信号機などがシーケンス制御でタイマーや条件分岐などをつかったプログラムによって機能しています。

対して、フィードバック制御とは制御対象の出力をフィードバック(入力側にもどすこと)することによってセンサなどによる測定値を設定した目標値と比較して近づけるように修正動作を行う自動制御のことをいいます。クローズドループ制御、閉ループ制御とも呼ばれます。身近な例ではエアコンの温度設定などですが、自動車の運転も視覚などの情報をもとにして脳で判断してコントロールしているのでフィードバック制御といえます。

自動車のオートクルーズ機能は人がメータやエンジン音などから速度を感知してコントロールするかわりに車載センサが速度を検知してフィードバックしてエンジンへの出力を調整したフィードバック制御です。

フィードバック制御はシーケンス制御にはない長所があるわけですが、フィードバック情報を使っていることで、修正の仕方に不具合があると、とても不安定な状態になることがあります。つまり修正するための信号・情報が常に目標値に近づくものであれば安定してよいのですが、さまざまな要因(外乱)により目標値からかえって遠ざかる方向にいくとクローズドループのためいわゆる悪循環で不安定になってしまうことがあります。

現場でよく耳にするハンチングとは動きをともなう機械系のフィードバックシステムが調整不良により振動的になる現象のことで、また、ハウリングと呼ばれる現象はマイクが音声以外で出力先のスピーカーから発した音まで拾ってしまいクローズドループを構成してしまって不可抗力的に増幅してしまい不安定な状態になっていることをいいます。

このため、フィードバック制御を設計するための大事な項目として、まず安定性、つぎに目標値への追従性を求めるのです。この他、さまざまな変動要因や外乱、ノイズなどに対しても強い外乱抑制性(ロバスト性)などが求められることもあります。

フィードバック制御の設計は、古くから理論が確立されていて学問にもなっているものですが、一般の人が予備知識なしにいきなり「制御工学」と呼ばれる書物や教科書などをみても内容はほぼ数学的で抽象的なものなので理解することは困難で、正直まったく面白みを感じないかもしれません。

最近でこそ、インターネットの普及でこの難解で抽象的なものを具体的な例でいろいろな角度から説明をしているのも見られるようになったので、本気になれば独学でも勉強できるようになってきましたが、やはり数式主体のものはなじみにくいものです。

そこで、当サイトではできるだけ数学的なものに頼らずに特にモータの制御をテーマとして具体的で本質的なところを解説していくつもりです。が、それでも本質を表すある程度の数学・物理学的で説明するのに避けて通ることができないところはでてきますのでそこのところはしっかりとがんばって理解してください。
制御理論の分類

制御理論は学問的には古典制御と現代制御とに分類されます。
古典制御は端的にいうと伝達関数モデルをベースに考える周波数領域(複素数空間)で評価解析する制御理論です。対して、現代制御理論は状態空間モデルをベースに時間領域(実数空間)で評価解析する制御理論です。



これらは名前が表しているような古いとか新しいとかの分類で捉えるのではなく、制御に対するアプローチが違うもので、どちらも一長一短あります。その他、派生したものでロバスト制御、適応制御などがありますが、これは古典、現代理論を発展させた制御手法です。

当サイトではいわゆる古典制御と呼ばれる周波数領域(複素数空間)で解析するものを取り上げています。私が電気系出身であることに加え、伝達関数をベースにする考え方は入力と出力間にある種の特殊なフィルタを構成するという考え方でどちらかといえば数学的でなく物理的に設計できるところが性に合っています。


現代制御理論は時間領域で解析するのが基本でどちらかといえば数学的で制御対象を状態方程式と呼ばれる微分方程式で構成するモデリングをしてからの解析です。微分方程式を解くのは難解ですが、コンピュータに解析させればよいのでそこは問題ではありません。古典制御に比べてモデリングパラメータにある程度精度が求められます。状態方程式で使われている状態変数を扱っているため多入力他出力システムとして解析できます。

両者の特徴を端的にまとめると、システムの安定化等の設計評価をするのに、伝達関数をベースに周波数領域の複素数空間でおこなうものが古典制御理論で、微分方程式である状態方程式をベースに実際の時間空間で数学的な解析、設計を行うものが現代制御理論です。物理的な評価を重視するには古典制御がわかりやすく、計算重視で内部パラメータの高度な解析をするには現代制御が向いていると思いますが個人の好みにもよります。

例えば台車式の倒立振子の事例では振り子の角度や台車の位置を状態変数としてアクチュエータのトルク等を操作して出力の振り子の角度をコントロールするものですが、入力に対して出力までが複雑な関係になっていて伝達関数ひとつで簡単に特性が見通せるものではありません。

この例では入力から出力までに多数の変数が存在していて、それらの状態を把握できる現代制御理論が向いています。状態フィードバックを適切に施すといとも簡単に安定化できます。伝達関数を用いた古典制御理論でも可能ですが少し無理があるようです。

現代制御理論は古典制御理論にはない利点もあるのですが、どちらかといえば数学的な解析のものですので、制御を学ぶ初心者で、数学的な解釈が得意な人であれば現代制御理論から学んでもよいのですが、物理的な解釈を重視したい人であれば古典制御理論から入るのがよいのではないでしょうか。肝はそんなに難しくないので。

個人的な見解では現代制御理論と古典制御理論はそれぞれの利点を活かすために、二分して捉えるのではなく、用途により融合して利用するのが最強であるように思われます。例えば、大規模で複雑なシステム全体を最適に管理制御するのに現代制御理論を活用し、そのシステム内で使用される個々のパーツレベルの制御には古典制御理論を活かして性能を確保するイメージです。
制御理論を理解するための前準備
古典制御理論とよばれるものは、実時間領域の制御モデルを周波数領域(複素数空間)の伝達関数に表現してから評価解析するものです。ここでは理論内容を理解するために複素数の概念を始め、ラプラス変換と呼ばれるツールの使い方を理解して伝達関数モデルに変換してからブロック線図まで作成することを目的としています。

制御理論を解説しているものはとかく数式を多用して解説しているものが多いのですが、当サイトではDCモータを使用したモーションコントロールを実現するに必要とされる最低限のものに絞って解説を行っていますが実用的には十分なものです。
複素数について

数学ででてくる虚数とは二乗するとj2=-1になる数j(電気・制御工学では電流iと区別するためjとしています)というだけのなんやらとても抽象的で無味乾燥な概念を持つものですが、この虚数の概念を物理学に手段として応用するととても便利なものに化けるのです。

複素数zとは実数部aと虚数部jbが組み合わさったz=a+jbとしたものです。実数空間では例えば電流i(t)はパラメータt(時間)による増減だけのスカラー量(大きさそのもの)ものであったのに対して複素数空間ではZ=a+jbのベクトル量(大きさと位相をもつもの)で表現できるようになります。


つまり、Z=a+jbでは虚数部bは実軸上のaに対して90°反時計回りの虚軸上にあることを表しています。ある複素数に虚数jをかけるとその複素数のベクトルは原点を中心に反時計回りに90°回転した位置になる(位相が90°進む)特性があります。

この特性を活かして、電気回路や運動方程式を複素数空間に変換すると、実数空間で表現する(微分方程式の世界)よりずっと解析しやすく扱いやすくなります。 ちなみに高校までの物理学では複素数の概念を用いることはなく大学で初めて登場します。

工学で使う複素数は数学的な本質的なものではなくその特性を利用した便利なツールとして使うものと考えたほうがよいです。
電気回路で複素数が使われる理由

電気工学では回路を解析するのに複素数平面が使われます。抵抗値Rだけの直流回路であればいわゆるオームの法則が成り立つ実数のみで扱えるので誰でも直感的に理解できます。これに対して、コイルLやコンデンサCで組み合わさった交流回路の場合は単純に実数のオームの法則だけでは動作が説明できません。

というのもコイルLとコンデンサCでは流した交流電流(正弦波)に対して電圧の位相がコイルでは進み、コンデンサCでは遅れるからです。そこで、電流や電圧の実効値のみならず位相の情報も含めることができる複素数平面を用いると回路をベクトルで扱うことができシンプルになるからです。
ちょっと話がそれますが、なぜコイルとコンデンサでは電流に対して電圧の位相がずれるか数式を使わずに物理的に考察してみます。

コイルL、コンデンサCでは位相がずれるものを数式であらわすと以下のようになります。この数式は時間変化のある回路で有効のものです。コイル、コンデンサに流れる正弦波の交流電流に対してそれぞれ両端にかかる電圧の位相がコイルでは90°(π/2)進み、コンデンサでは90°遅れるのがわかります。これを複素数空間で表していくことにします。
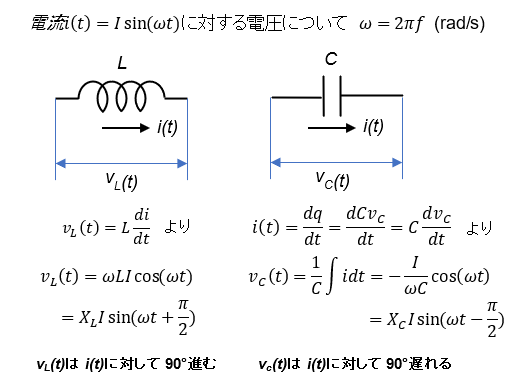
抵抗値Rだけの直流回路では抵抗は実数分のみであったのに対してコイルLやコンデンサCで組み合わさった交流回路ではインピーダンスZといって抵抗R分に加えてコイルの誘導性リアクタンスXL(=ωL)によるインピーダンスZLはjXL、コンデンサの容量性リアクタンスXC(=1/ωC )によるインピーダンスZCは-jXCなので、抵抗R、コイル、コンデンサが直列につながったばあいは全体のインピーダンスは
Z = R + j(XL-XC) = R+j(ωL-1/ωC) なる複素数のベクトルです。
もとのベクトル成分にjをかけることは位相が90°進むことを表し、-jをかけることは位相が90°遅れることを表します。
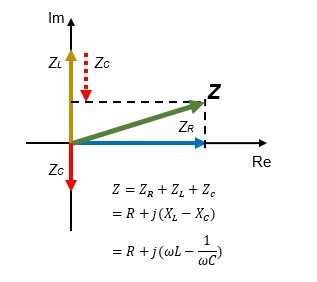
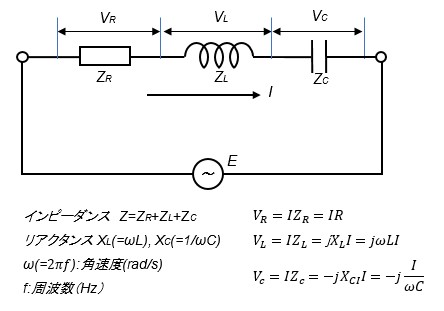
共通の電流が流れる直列回路ではインピーダンスZの定義式より抵抗Rにかかる電圧VRの位相に対してコイルにかかる電圧VLの位相は90°進み、コンデンサにかかる電圧VCの位相は90°遅れます。
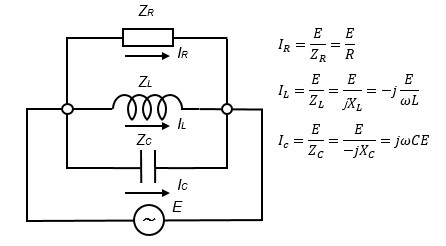
電圧を共通とする並列回路では抵抗、コイル、コンデンサに流れる電流はコイルでは位相は90°遅れ、コンデンサでは位相は90°進みます。
この複素数ベクトルを扱うと、入出力間の周波数特性や、位相特性も比較的容易に解析することができるようになり大変便利です。
制御理論においてわざわざ周波数領域の複素数空間で設計をおこなう理由

入力から出力の間を伝達関数として扱ういわゆる古典制御においては入力を目標設定値、出力を制御目的の物理量として、伝達関数を含むシステム全体を周波数領域の複素数空間に変換して解析しています。
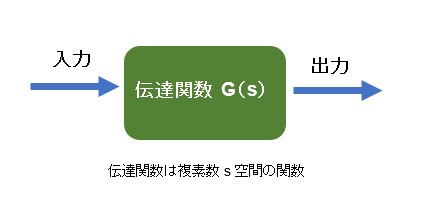

伝達関数を作成するにはまず、制御対象を数式でモデリングする必要があります。これは古典制御理論でも現代制御理論でも同様です。電気回路でも、力学の運動方程式でも、実時間領域でモデリングすると時間をパラメータとした微分方程式となります。

制御対象を解析するのに微分方程式を解く必要がありますが、制御対象が複雑になるほど解くのが煩雑な上、数字上の計算なので実態がつかみにくくなります。また、解に複素数が含まれた場合は時間tの関数で表されても実際には存在しない抽象的なもののため、どういった挙動をするかを理解しにくいものです。

そこで、微分方程式を解く手段として、複素数sを利用したラプラス変換というものがあり、これを使うと、難解な微分方程式が代数方程式に変換され、また、パラメータを複素数空間で表すことにより、挙動を直感的に把握することができるようになります。実際に制御対象をモデリングしてラプラス変換することにより、微分方程式のモデルを周波数領域の伝達関数を作成することをやってみます。
制御対象のモデリング
① モデル1 抵抗RとコンデンサCを組み合わせたRCフィルタのモデル

電気回路をモデリングする場合には微分方程式で表現することはできますが、電気工学でおなじみの複素数で表したインピーダンスを用いて複素数空間でのモデルを直接作成するほうが容易ですので両方でモデルを作成してみます。下図の①が実時間空間の微分方程式による回路のモデルです。対して②は複素数空間での回路のモデルです。
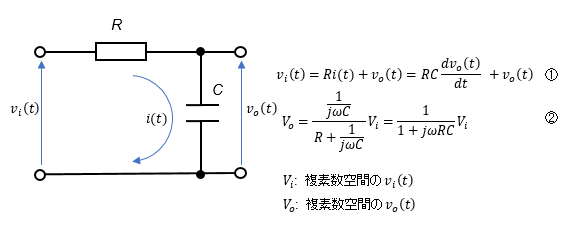
② モデル2 DCモータの回路モデル(電気回路)

DCモータ電気系の微分方程式モデルが①で複素数空間モデルが②です。
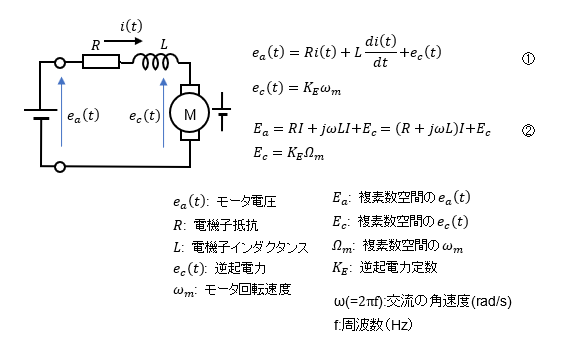
③ モデル3 DCモータの機械系モデル(運動方程式)

機械系のモデルはまず一般的にニュートンの運動方程式により微分方程式モデル①が得られます。


これらの例では、実時間空間の微分方程式によるモデルと複素数空間のモデルが得られました。古典制御理論ではこれらをすべて複素数空間で解析するのでモデルが実時間空間の微分方程式の場合は複素数空間の伝達関数として表すために、ラプラス変換というツールを使って変換します。
ラプラス変換:(時間空間から複素数空間への変換)

制御工学でのラプラス変換の目的は実時間t空間の微分方程式を複素数s空間の代数方程式に変換して計算や解析・評価を容易に扱えるかたちにすることです。ラプラス変換の変数sはラプラス演算子といって微分演算子に相当するものでjωをsに置き換えたものです。 ラプラス変換すると数式化したモデルは多項式で構成される伝達関数のブロックとして入出力特性、周波数特性を調べたり、安定性を判別したりできるようになります。

このラプラス変換そのものはあえて数学的な内容を理解しないでも使えるもので、あくまで解析手段として利用するものだと割り切ったものでもよいと思います。初めはあまり数式にとらわれないで数学的意味はある程度慣れてから理解を深めたい場合は内容をたどってもよいと思います。

ラプラス変換による複素数空間に変換した伝達関数を設計評価したあとは、最終的に逆ラプラス変換により時間関数に戻して実際の動作を確認します。逆ラプラス変換を手作業の計算で行って時間関数に戻せば、マイクロソフトExcelなどを使ってシミュレーションで評価ができますが、現在ではシミュレーションアプリを利用すれば、数学的なことを一切せずとも最終評価までできてしまいます。

実用的な面では、手作業の計算式によるシミュレーションはせいぜい2次遅れのシステムまでである程度複雑なものになるとシミュレーションアプリケーションを使うのが便利で確実です。そうなると、数式的なところはあまり意識しなくても使えますので、制御の本質な部分にだけ集中できます。言い換えれば複素数のs空間でだけ意識して制御の設計ができるということです。
何をしているかの本質をつかんでさえいれば、手段を問わず、一番合理的な方法で結果をだせばよいのです。
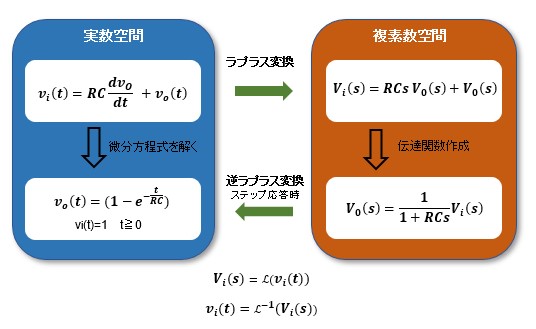

時間関数f(t)から複素数関数F(s)へのラプラス変換ではf(t)が時間tの関数であるのに対して、ラプラス変換後のF(s)は複素数sの関数です。電気回路のモデル1において微分方程式①では微分項をsとして複素関数に置き換え、すでに複素数空間で作成した②ではjωをsに置き換えるとラプラス変換結果と同じにものなり、両者は一致します。

ラプラス変換の公式はいくらかありますが、試験や研究のためでもない限り、覚えるべきものでもありません。モーションコントロールで使うラプラス変換をするのにとりあえず知っておくべきものは限られていてそれらを下記にまとめました。

電気系、機械系の微分方程式をラプラス変換するには1次微分、2次微分および積分を使えばモデリングでき、伝達関数の基本形として1次遅れおよび2次遅れ伝達関数の特性を理解しておけばよいと思います。1次、2次とは伝達関数分母多項式の次数のことです。


実時間空間でのシミュレーションでは入力信号としてステップ信号やランプ信号で評価することが多いので以下の公式を知っておけばよいと思います。
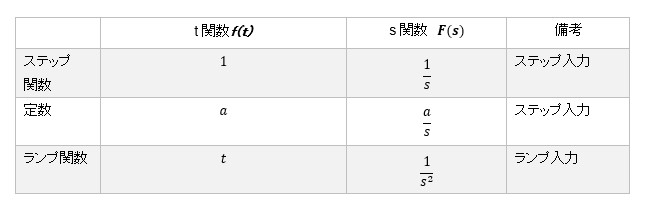

伝達関数G(s)をシミュレーションのために実時間空間の時間関数g(t)にするには逆ラプラス変換を使用します。

手動で計算する場合は例えば入力信号u(t)がステップ信号であれば、G(s)U(s)=G(s)/s、ランプ関数であればG(s)/s2として逆ラプラス変換します。手作業でシミュレーションをする場合に1次遅れと2次遅れ系のステップ応答時間関数を記載しておきます。

伝達関数によるブロック線図表現

制御対象のモデリングで作成した数式モデルにラプラス変換をして複素数s空間のモデルに変換して伝達関数としてブロック線図で制御対象を表現します。s空間でのブロック線図では入力から出力間の信号伝達の様子がフローチャートのように機能ごとに分類されて視覚的に分かりやすく表現されています。
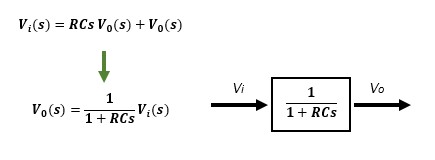
① モデル1 抵抗RとコンデンサCを組み合わせたRCフィルタのモデルのラプラス変換
微分方程式で表されたRCモデル①にラプラス変換を施してブロック線図で表します。入出力間の伝達関数は時定数RCの1次遅れ系になっていることがわかります。
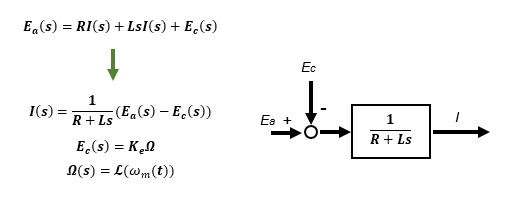
② モデル2 DCモータの回路モデル(電気回路)のラプラス変換
微分方程式で表されたDCモータ電気系モデル①にラプラス変換を施してブロック線図で表します。出力電流Iは入力をモータ電圧Eaとすると逆起電力電圧ECが返される1次遅れ系となっているのがわかります。
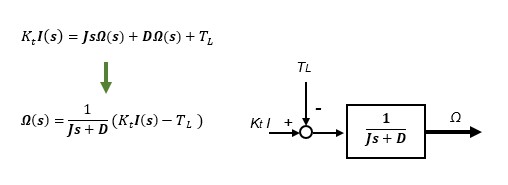
③ モデル3 DCモータの運動方程式(運動方程式)のラプラス変換
微分方程式で表されたDCモータ機械系モデル①にラプラス変換を施してブロック線図で表します。出力のモータ回転速度Ωは入力トルクKtIが負荷トルクTLとつりあう1次遅れ系の特性であることがわかります。
これまでで、フィードバック制御を周波数領域で評価解析するための、モデリング、ラプラス変換による伝達関数作成、およびブロック線図の作成について解説してきました。次章【解析編】ではブロック線図の見方および伝達関数の基本形である1次遅れおよび2次遅れ系の特性を解説してから、いよいよフィードバック制御システムを設計するための勘所をできるだけ数式と物理的な観点を合わせて解説していきます。
周波数領域で特性を設計評価したあとは、時間領域でのシミュレーションにより実際に近い動作を確認するのですが、そこでおすすめなのがScilab(サイラボ)と呼ばれるオープンソースのシミュレーションアプリです。記述は運動方程式など微分方程式でも、伝達関数で構成したブロック線図でもよく、時間応答のみならず周波数応答のボード線図も作成してくれるすぐれものです。
このような便利なツールがあるおかげで、難解な微分方程式を解いたり、ラプラス変換表をもとに時間関数へ変換して解析しないでも結果をだせるようになりました。その恩恵を受けてフィードバック制御本質の部分に集中できるので制御理論と呼ばれる敷居が下がってすこしは身近になったのではないでしょうか。