インパルス応答とその伝達関数の物理的解釈

システム入出力間の時間領域における関数g(t)が入力信号に応じてどのような特性をもつのか検証してみました。この検証のためにはインパルス応答というものが必要ですので、まずインパルス信号について要点を押さえていきます。インパルス応答は機械系のモーションコントロールを扱っているうえでは普段はあまり意識せずともよいところですが、制御理論としてはよく目にするものです。電気系システムの信号解析などにはよく使用されるかもしれません。
周波数領域であるs空間での伝達関数表記では入力U(s)、制御対象G(s)、出力Y(s)は分けて解釈できるのですが、時間領域の関数g(t)の特性は入力信号u(t)との合成、つまりy(t)=g(t)によるものなので実態がつかみにくいことになります。
そこでシステムにステップ入力を与えたときの応答と比較しながら、インパルス応答時の特性を調べて、数式的な解釈と物理的な現象ではどういうことを意味するのかを考察していきます。
インパルス入力の定義

インパルス入力は時間幅が無限小で、振幅は無限大、かつ積分すると1であるものです。実現はできませんが、数式の上でシステム特性を調べるのに有用です。

システムに対して瞬時に衝撃的なインパルス入力を与えるとその応答として安定して収束するのか、不安定になり発散するのか、いわゆるシステムそのものの特性が現れます。これがインパルス応答です。
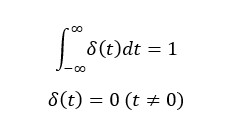

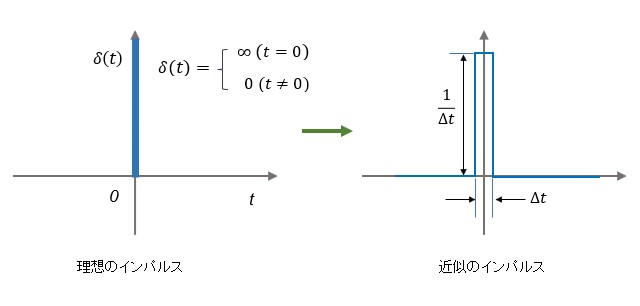
理想のインパルス信号は現実には生成できませんので試験等で使用するには近似したものを使用します。

インパルス信号はラプラス変換すると1となるのも特徴です。つまり、システム伝達関数のインパルス応答特性を時間領域に逆ラプラス変換する場合、s領域での入力は1なので伝達関数そのものの特性を調べることになります。これがインパルス応答の重要な部分です。
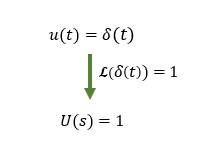
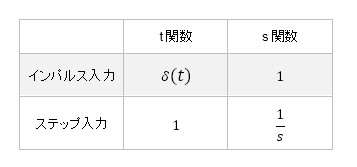
入力に対するそれぞれの応答

さて、インパルス入力というものがわかったところで、システムにステップ入力を与えた場合と比較していきます。

下の表に、システム伝達関数G(s)が、定数K、積分1/sおよび1次遅れ1/(1+Ts)の場合に、それぞれインパルス入力、ステップ入力を与えた場合の時間関数g(t)を記載しています。
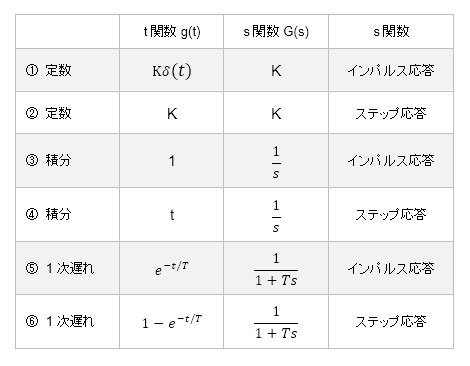

以下にシステムが定数、積分、一次遅れの場合に入力に対してどのような出力となるかを図解で解釈していきます。

s領域の伝達関数が定数の場合①②は時間領域のシステムも感覚通りに理解できます。例えば、伝達関数が定数Kの場合には入力が1の場合は出力はK倍のKになります。時間領域でも入力1に対して出力はKになります。どの条件でも出力は入力のK倍となります。
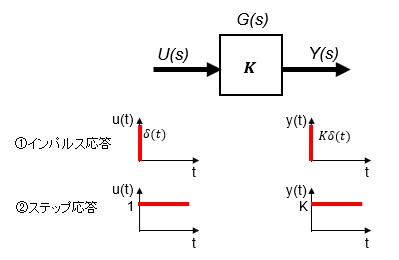

次は伝達関数が積分の場合③④です。数学的な解釈ではインパルス信号の定義や積分の意味からインパルス入力に対する応答は1の固定値で、ステップ入力に対する積分応答は出力が線形に増加することがわかります。s領域の伝達関数から解釈するとこのように理解するのに迷いはないとおもいます。

今度は逆に時間領域のシステムが1または定数の場合②③から考えてみます。つまり、g(t)=1(定数)の場合です。これは物理的にはどのような状態を意味するのでしょうか。ちょっと解釈に迷うところですが、入力に対して出力の変化がないこと、つまり、システムの時間経過において状態の変化がないことを意味しています。

ちょっと抽象的な表現のため、具体的な例を次節「運動方程式での解釈」で運動方程式を使って説明します。
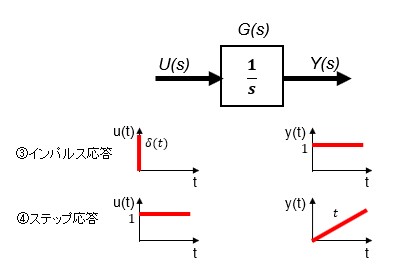

最後に、システムが一次遅れ特性をもつ場合⑤⑥です。積分特性に比べて直感的に動作を解釈しやすいと思います。
運動方程式での解釈

積分特性を物理的に解釈するために、摩擦を無視した質量Mの物体に外力f(t)を与えたときの速度v(t)について考えます。
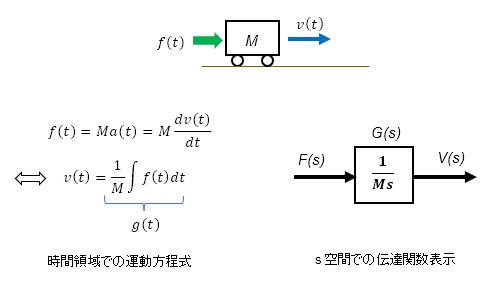

時間領域の運動方程式において、外力f(t)により生じる加速度a(t)は質量Mが一定であれば外力f(t)に比例します。つまり、入力を外力f(t)、出力を加速度a(t)とすると、入出力間の伝達関数は①②の定数に相当します。

物体の速度v(t)は加速度a(t)の時間積分ですので、外力f(t)からみるとv(t)は積分器を通したものになります。

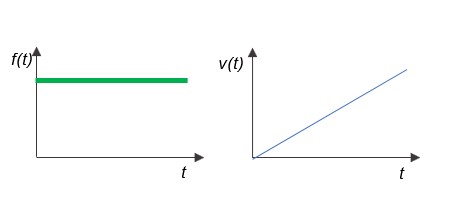
ここから本題に入ります。静止している物体に外力としてインパルス入力を与えると物体は初速度V0で運動を始め、摩擦がない空間では質量Mによる慣性によりV0の等速運動を続けます③。つまり、入力に対して時間経過において速度v(t)の状態変化はありません。

これが、時間関数g(t)が一定であるシステムにインパルス入力を与えた積分動作の物理的解釈です。


外力f(t)をステップ入力にした場合は、物体は一定の加速度a(t)で等加速度運動し、速度v(t)は線形に増加する積分動作④をします。

ステップ入力自体のラプラス変換は積分と同じ1/sになるため、積分システムにステップ入力を与えると1/s2の特性で出力はランプ関数になります。
高校物理の教科書や参考書でよく見かける水平投射はインパルス入力による初速度V0の等速直線運動で、鉛直方向は自由落下でステップ入力に相当する重力による加速度gの等加速度運動です。

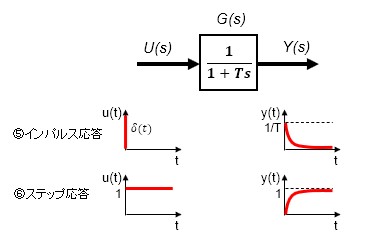
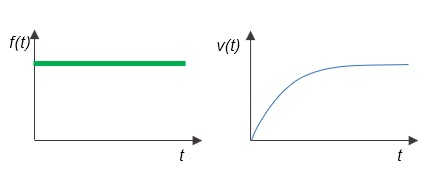
現実には摩擦が存在するので、外力f(t)をステップ入力で与えると、摩擦力と釣り合い、速度v(t)は1次遅れになります。
後記:
インパルス応答はシステムそのものの応答特性を検証するのに有用なもので、実用的なステップ応答と比較して解説しました。数式上では公式として当たり前のように使用しているものでも完全に理解していなければうまく説明できないことがあります。今回、焦点をあてたインパルス、ステップ応答と積分との組み合わせも意外と完全に理解できるまで手こずりました。他にもこのような事例があればできるだけ凡例をあげて解釈していきたいと思います。

