相補フィルタのしくみを解明してみる【加速度・ジャイロセンサ】
加速度・ジャイロセンサを組み合わせて使うのに相補フィルタがよく用いられますがその詳細に関する解説はあまり見かけません。どのような過程で相補フィルタの式が導かれ、式が何を意味しているかは知りたいところです。比較的単純な式の中には深い意味があるところを算出過程で解説していきます。
加速度センサとジャイロセンサは物体にかかる動きや回転の情報を検出するデバイスですが、特に姿勢位置を得るにはそれぞれ短所、長所があるため安定した情報とするのに一工夫する必要があります。
加速度センサは動きを検出するセンサで姿勢位置を得るにはx,y,z3軸にかかる重力からそれぞれ軸の傾斜角を算出できます。
ジャイロセンサは それぞれx,y,z3軸の角速度を検出できますのでプログラム内で積分させると動作角度を算出できます。
これだけだと物体の姿勢位置を得るのにそれぞれ単独で使用できそうですが、加速度センサは動きがある場合には重力以外の成分も加わるのに加え、出力が敏感で細かなノイズが含まれています。ジャイロセンサでは検出した角速度を積分するために誤差成分も累積してドリフト(オフセット)が生じてしまいます。
加速度センサ、ジャイロセンサの短所を克服して長所のいいとこ取りだけすると安定した姿勢が得られるのですが、その方法の一つに相補フィルタというものがあります。
相補フィルタの構成

相補フィルタをブロック線図で表すと下図のようになります。

加速度センサではノイズ成分を除去した低周波領域の情報がほしいためにローパスフィルタ(LPF)を通します。

ジャイロセンサでは累積するドリフト成分を除去するためにハイパスフィルタ(HPF)を通すと情報のドリフトによるオフセット分をキャンセルできます。
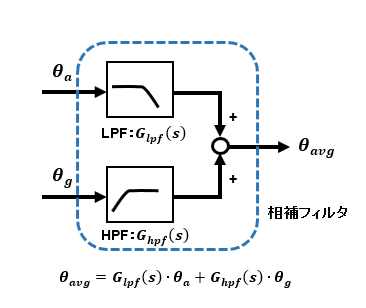

加速度センサあるいはジャイロセンサ単独にそれぞれフィルタを通すだけでなく、組み合わせることでいわゆる互いにいいとこ取りしあうところから相補フィルタと呼ばれます。

相補フィルタに使用するLPFとHPFには条件があり、任意の周波数でフィルタゲインの和が1であることです。

わざわざ相補フィルタを使わなくても、単独の加速度センサにはローパスフィルタ(LPF)を、あるいは単独のジャイロセンサにはハイパスフィルタ(HPF)を通すだけでいいようにも思われますが、これらの場合にはフィルタによる位相遅れが生じたり、入出力間で信号情報ゲインが変化してしまいます。2つのセンサの長所を利用することで理想の出力が得られるのがこの相補フィルタの利点です。
相補フィルタの周波数特性

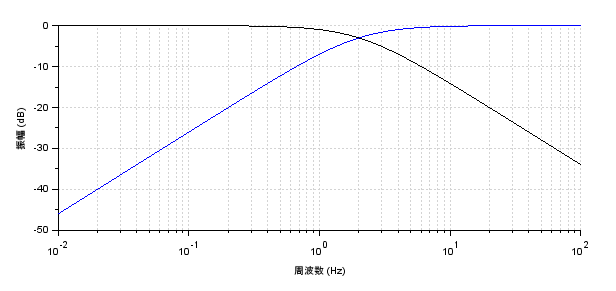
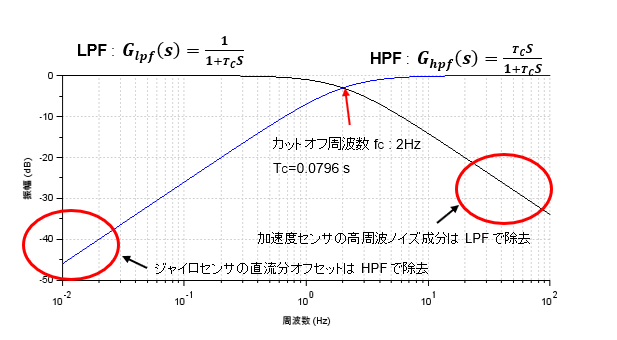
相補フィルタのLPFとHPFでカットオフ周波数を2Hzとした場合の特性を周波数領域のボード線図で表すと下図のようになります。縦軸はゲインを表していて単位はdB(デシベル)ですが、この条件ではLPFとHPFのゲインは足すと全領域で1となります。

LPFはカットオフ周波数fc以上の高周波成分を除去しますので加速度センサからの情報は低周波部分のみが残ります。

HPFはカットオフ周波数fc以下の低周波成分を除去しますのでジャイロセンサからの情報はゆっくりしたドリフトによるオフセット分が除去されます。

カットオフ周波数fcが2Hzとした場合はほぼジャイロセンサによる情報が優勢になります。最終的には出力を見ながらfcを微調整をすればよいと思います。
相補フィルタの算出過程

相補フィルタは結果の式だけ知っていれば使用はできるのですが、式の意味を知らなければなんとなくの当てずっぽうで係数等のパラメータ値を決めることになります。

相補フィルタを使用するのであればやはりある程度式の内容は理解しておきたいものです。


ここでは1次遅れフィルタ、ラプラス変換などの概念がわかっていれば理解できます。
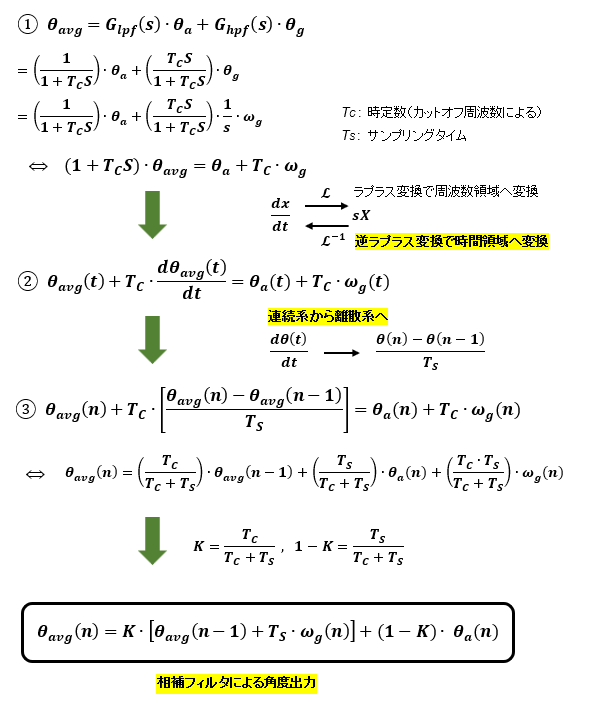

ようやくよく目にする相補フィルタの式を導きました。これは1次フィルタの場合です。これで重み係数Kの意味もわかると思います。

係数Kはカットオフ周波数fcとサンプリングタイムTS で決まるものです。
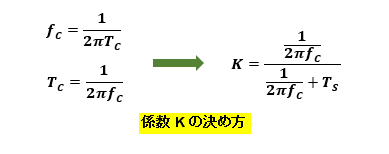

一般的に出回っている相補フィルタ情報の中には加速度センサとジャイロセンサの出力に係数Kを重みとしてかけた解釈のものもありますが、これでは意味をなしません。
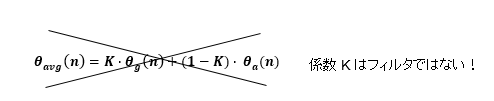
結果だけをみると、相補フィルタの式は比較的シンプルな形になっているのですが、実はこれだけの意味が含まれていることが理解できると思います。式の内容をブラックボックスでなく理解できていると安心して使用できるようになると思います。相補フィルタの発想は天才的で感動すらあります。



