マイコンで実現するフィードバック制御のための基礎知識【番外編】

倒立振子は現代制御理論の典型的な教材です。一般的に出回っている情報では学術的すぎるか、試行錯誤的すぎるかのものが多く初心者でも理解できるように体系的に検証したものはあまりみられないため、実践で使えそうなものに絞りまとめてみました。さらにロバスト制御を適用し、より実用的な検証をしてみました。
目次
現代制御理論の適用

これまで伝達関数をベースとしてフィードバック制御について検証してきました。いわゆる古典制御でのアプローチです。制御できるのは原則として1入力1出力の制御対象システムで温度コントロールや単体モータのモーションコントロールなど身近なフィードバック制御の大部分はこれに適しています。


これに対して、少し複雑なシステムで典型的なものが倒立振子の制御があげられます。台車型の倒立振子を例にとると、倒立振子はもともと不安定なものなのですが安定した倒立状態を保つためには台車の位置を微調整して常に振子の重心位置とのバランスをとることをします。

制御の目的は振子の倒立角度を台車に対して垂直にすることですが、間接的な台車の位置も同時に制御するために押す力などを入力とするいわゆる1入力多出力のシステムとなっています。

古典制御のPID制御などでゲインを適切に設定し、台車位置と振子角度を同時に制御することは不可能ではありませんが、場当たり的な調整では大変なうえ、かえって制御システムを複雑にしてしまいますので無理があるようです。

このような台車位置や振子角度のような複数の変数を同時に安定化させるのに適したものが現代制御理論です。現代制御理論ではシステム内部で扱う複数の変数を状態変数とよび、これらを同時に安定化させるための理論です。


現代制御理論の解説書をよむと数学的なものなので独学するとほぼ間違いなく心が折れてしまいますが、勘所さえわかっていれば本質は決して難しいものではありません。

数式を理解せずとも今ではフリーで便利なツールが利用できるので実際にいろいろ試すことができ難解と思われがちな現代制御理論を理解することも容易になりました。

そこで、現代制御理論の典型的な適用例である倒立振子を通してこの理論のすごいところを確認していきたいと思います。
倒立振子とは

倒立振子には大別すると2種類あり、台車上に支点のある振子を搭載した台車型と2輪軸に振子の支点がある車輪型があります。
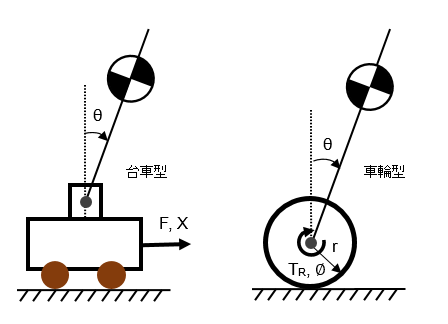

台車型倒立振子は台車の位置Xを、加えた推力Fにより調整して振子角度θをゼロに近づけるもので運動方程式も比較的簡単で台車と振子の干渉もそれほど多くなく制御もしやすいといわれています。

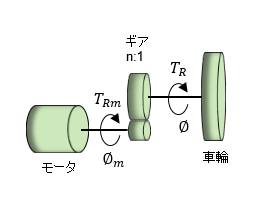
対して、車輪型倒立振子は車輪の回転角Φを、トルクTRにより調整して振子の角度θをゼロに近づけるものですがトルクTRが車輪の並進とともに振子の回転にも影響を及ぼし互いに干渉し合うために運動方程式は少し複雑になっています。
車輪型倒立振子運動方程式

本編では倒立振子に現代制御理論を適用して、その有用性をシミュレーションにより検証していくのですが、後にLEGOの実機を使って検証したいのでそれに合わせて 車輪型倒立振子を取り扱います。

車輪型倒立振子の運動方程式は結構複雑で算出するのは大変なのですが、ここでは 以下のモデルで算出過程は省いてできあがったものを使用します。
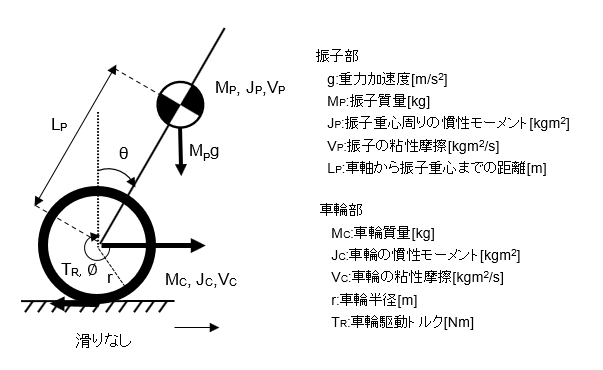

①は車輪、②は振子の運動方程式です。これらを導くのに以下の近似と線形化をしています。
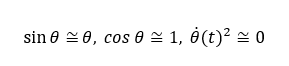


入力はモータへの電圧あるいは電流で、駆動する車輪はモータ軸からギア等伝達機構により連結していて、それらをすべて含むと①式は以下の①'になります。車輪および振子の質量やモーメントが影響しあって複雑な式になっています。
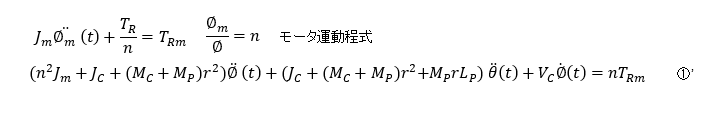
近似モデル方式

制御をするにはまずベースとなる数式モデルが大事なのでこれまで頑張って運動方程式を導いてきました。

通常、学術論文などでは導いた運動方程式①’に基づいてトルクを計算して相当する電圧や電流に変換した入力としているみたいですが、実際のところモータ軸慣性や粘性摩擦等を取得するのが困難なうえ、仮にすべてのパラメータが取得できてもパラメータの変動はつきものでトルク計算方式によるものは実用的な観点からは??な気がします。

つまり、制御したいのは振子角度や車輪あるいは台車の位置なのですが、いくら複雑な数式からトルクや推力を求めてもそれらは間接的であってあまり信頼できないのです。

そこで、マイコンで実現するフィードバック制御のための基礎知識【発展編】で近似モデルの解説をしましたが、ここでも電圧か電流入力uから出力の車輪速度までを1次遅れで近似した伝達関数を使用します。


これで車輪の運動方程式①"はすごく単純で実用的なモデルになりました 。 ただし、振り子による干渉項(①,①'式の2項目)は無視しています。振子の運動方程式②はまだ複雑なままですが、今回はまだシミュレーションの段階ですのでパラメータは既知であるとします。

実装する場合には振子の部分も近似モデル化するのですが、振子のパラメータとして大事なものは周期と減衰の特性ですのでこれらのパラメータだけでも同定を行い取得することになります。

運動方程式①''②を変形して状態方程式③④の形にします。これが車輪モデルを近似した車輪型倒立振子の状態方程式です。
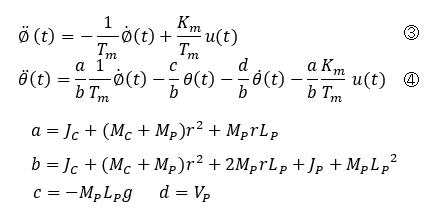
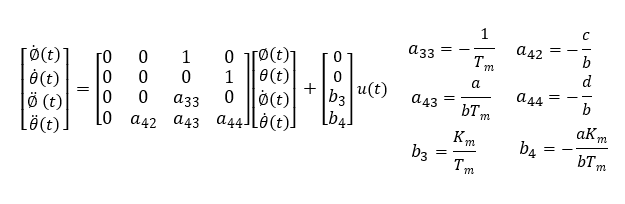

現代制御理論で検討するために下記の形式になおします。現代制御では見慣れた形式でこうしてようやく解析を開始できます。


この方式の問題点は近似化するにあたり、振り子の影響を無視していることです。つまり、入力uが電圧や電流では車輪速度は実際には振り子の動作が外乱負荷として多少なりとも干渉するということです。これを解決するのが次に解説する車輪速度入力方式です。
車輪速度入力方式

前回の車輪近似モデルを用いた倒立振子でも十分実用的になったのですが更に一歩すすめて、今度は入力がこれまでの電圧や電流でなく、車輪速度である場合で検討します。

モータの電圧や電流を入力とした場合は、簡素化はしたのですが、振子の影響(干渉)が車輪に及ぼす問題は解決はされていませんでした。そこで今度は車輪速度を入力とした速度制御系にすることで車輪は振子の影響をうけないロバスト性を高めたものになります。
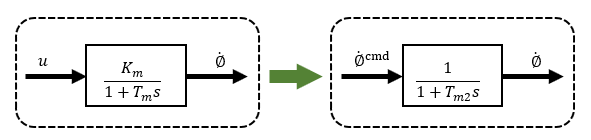

以前DCモータのロバスト制御で解説したとおり、2自由度制御とすれば完全なロバスト制御となりますが、今回は簡易なハイゲインフィードバック方式による車輪速度制御で検討を行います。
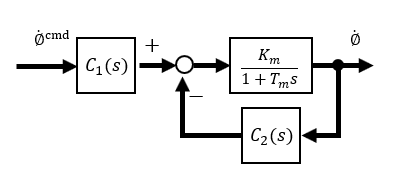


車輪速度制御にて車輪速度入力に対して出力が1次遅れとなる場合の状態方程式は⑤⑥になります。車輪の方程式は任意に設定できる時定数Tm2だけがパラメータとなっているのが特徴です。

ハイゲインフィードバック方式なのでロバスト性はフィードバックゲインC2が大きいほど向上しますが、同時に時定数Tm2にも影響するので小さくなりすぎないように実現できるレベルで設定します。
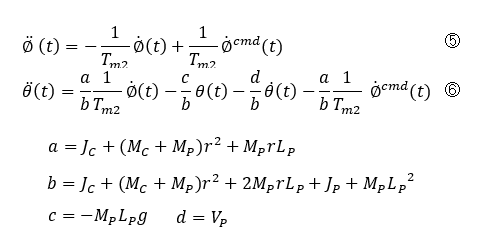


現代制御理論形式の状態方程式です。形式的には電圧や電流を入力とした近似モデル方式と似ていますが、内容は全く違います。

外乱抑制を向上した車輪速度制御系になっていますので車輪速度は振り子の影響を受けずに指令入力に追従します。これまでのように車輪のトルクではなく車輪の速度により振り子を安定化させるところが異なるポイントです。
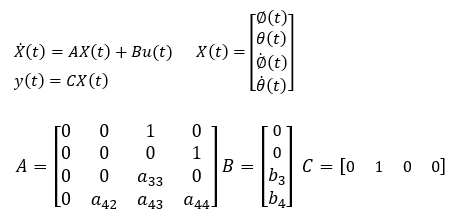
状態フィードバックによる安定化

現代制御理論では扱う各状態変数にゲインを乗じたものを入力へ戻す状態フィードバックを施すことで不安定なシステムも安定化することが可能となります。

これにて、システム全体のもともとの行列Aが不安定(行列Aの固有値が不安定)なものであっても状態フィードバックを施した行列A-BFはゲインを適切に設定すると安定させることができます。

システム行列の固有値は古典制御における特定方程式の解と同等のものですべての固有値が安定であることは状態変数が時間経過とともにゼロに収束することを意味しています。

現代制御理論では可制御性や可観測性などの評価が必要なこともありますが、ここでは両方とも可能なものとしています。
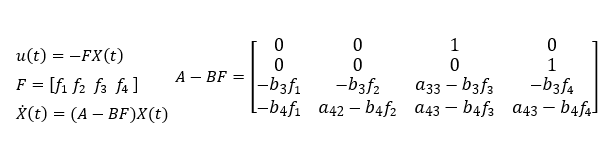
極配置法

古典制御において伝達方程式の特性多項式の解がすべて安定になるように極配置をおこなったことと同じく、現代制御理論においても極を任意に設定して状態フィードバックゲインを算出しシステム行列の固有値すべてを安定させる方法を極配置法といいます。

安定した極は実数部が負であることはわかるのですが実機にて実用的な動作を実現するための値設定をどのように決定すればよいかが定量的にはよくわからないものです。ある程度試行錯誤的なところはあります。そこで定性的かつ定量的な評価として用いられる方法が次に説明する最適レギュレータです。
最適レギュレータ (LQ最適制御)

極端なはなし、極配置法にて当てずっぽうで配置しても何が正解かはわからないため、評価の指標が欲しくなります。こんなときに一つのツールとして威力を発揮するのが最適レギュレータです。

最適レギュレータの数学的なことはさておき、式の意味するところは各状態変数の収束性と入力エネルギーuの消費抑制の評価指標をJであらわし、目的はJが最小になるように極配置されるフィードバックゲインを取得することです。

各状態変数に対する重みQでどの変数の収束性を重視するかで値を大きく設定したり、小さく設定したりします。 収束性を重視すると多くの操作量を必要とするので実現できるかを考慮するとやみくもに大きくもできません。 エネルギー消費の重みrは通常1にしておくことが多いそうです。

最終的な重みの決定はシミュレーションソフトや実機などで調整していくところです。極配置法に比べ、評価の指標があるので調整の目安となるところが現実的です。


シミュレーションソフトScilabを使用すれば極配置法においては任意の極を指定し、最適レギュレータおいては任意の重みを指定すればそれに応じた各状態変数のフィードバックゲインを算出してくれますので設計が簡単です。

難しい数学的な評価はさておき、ある程度簡単に現代制御理論を使うことはできるようになりました。
現代制御理論も古典制御理論と同様に勘所さえ押さえてしまえば決して難しいものではありません。数式的な意味合いはさておき、現在では便利なシミュレーションアプリケーションがフリーで使用できるのでどんどん活用してみるのも制御理論を理解する上での近道です。
シミュレーション

最適レギュレータで重みをQ=diag[5 5 1 1] 、r=1に指定して評価取得したゲインはF=[-2.2 -103 -3.2 -12.6]となったのでこれで設計したブロック線図は下図のようになります。
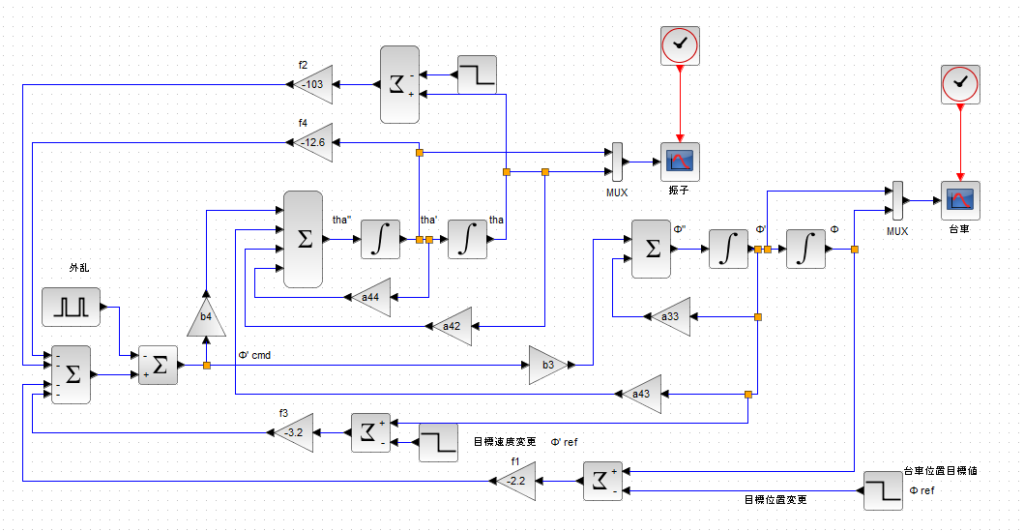
シミュレーション条件パラメータ:
MC:0.06kg / MP=0.6kg / LP=0.065m / r:0.04m / Tm:0.1s / Tm2:0.03s / Km:10 / vp:0.03kgm2/s JC:MCr2/2 JP:1/3MPLP2

通常、状態変数Xは時間経過とともにゼロに収束するのですが、ここでは車輪位置(角度)を目標値 Φref として5に設定(Φ’=Φ-Φref)したときの応答を示します。目標値がゼロ以外の状態変数車輪位置ΦはΦ’に相当します。

状態フィードバックした入力u(t)が以下のような車輪の速度指令になっているところが特徴です。
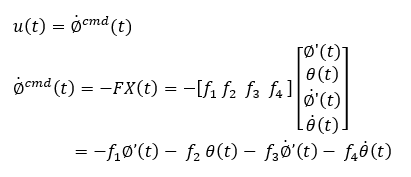
状態フィードバックを施したシステムにおける目標値について:
システム内の状態変数は互いに干渉するものなので複数の互いに独立した任意の目標値に設定することはできません。例えば、台車の車輪位置を目標値とする場合は速度はその微分したものに収束しますので、目標値がステップ状であれば、目標速度は0でなければなりません。車輪速度を目標値としてステップ状のものに指定した場合、車輪位置は同時にその積分したランプ状の目標値に指定しておかなければつじつまが合わなくなります。つまり、車輪位置と速度の目標値は常にセットで指定します。

実機においても、このような状態で運転できれば安定して倒立させながら同時に車輪の位置を変更させることができることを意味しています。

ちなみに、状態フィードバックを施す前のシステム行列Aの固有値は[-8.2 6.2 0 -20.0]で正の値が含まれるので不安定なのですが、施した後の システム行列A-BFの固有値は[-29.2 -7.5 -6.5 -1.6]ですべて安定な値となっています。

これは、状態フィードバックを施す前のシステム行列Aつまり車輪型振子は何も入力しなければ不安定な状態のままで、これに状態フィードバックを施した入力を与えたシステム行列A-BFでは振子の倒立も車輪位置も同時に安定していることを意味しています。
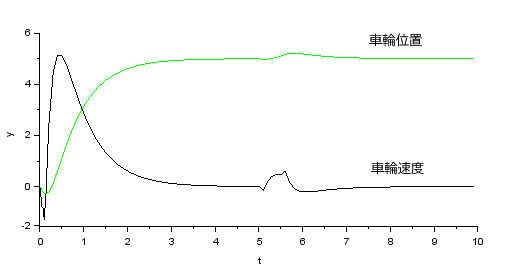
車輪位置および速度応答:

振子角がゼロ(垂直)で起動した直後は一旦振子を前かがみにさせるために車輪位置は瞬時に後退していますが、目標値5に収束するようすが現れています。

5秒目で入力にパルス状の外乱を加えたのですこし乱れますがすべての状態変数は安定して収束しています。
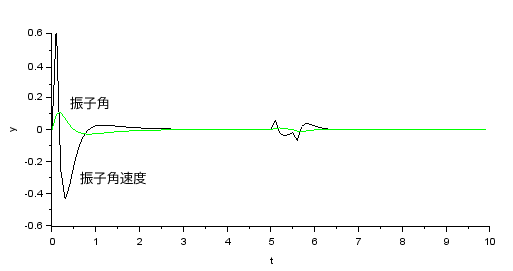
振子角および角速度応答:

振子角は起動時に前かがみになってからすぐにゼロに収束しようとし、わずかなアンダーシュートはみられますが安定しています。外乱を与えても収束しています。
一般に出回っている倒立振子の制御では新規性もなく面白みにもかけるのでより実践的なモータのロバスト制御を取り入れたいわば古典制御とのハイブリット的な観点で整理してみました。次は実機を用いていろいろ検証してみて最もシンプルで安定しているものを探求してみたいと思います。
倒立振子は古典制御によるアプローチで伝達関数だけで評価設計するにはどうしても難しかったので現代制御理論を取り入れてみました。現代制御理論は航空機・人工衛星やドローンの姿勢制御など高度で複雑なシステムの制御に向いているもので、一般に実用的なものかどうかはわかりませんが、理解しておくと役立てるときがあるかもしれません。



