STM32マイコン Nucleoボードを使った温度計

安価なサーミスタをセンサーの素子として使用した温度計をSTM32マイコン(Nucleoボード)で実現するアプリケーションを作ります。簡易なプログラムですがCortex-M3コアマイコンで浮動小数点演算を使ったアプリで他にいろいろな算術演算アプリにも発展できます。

サーミスタは温度により抵抗値が変化する特性をもった素子で温度計に適しているのはNTC特性をもったものです。 NTC特性のものは温度上昇につれ、抵抗値がゆるやかに減少するタイプですが、直線的な変化でなく非線形な特性となっています。

今回使用するサーミスタは103AT-2でB定数は3435K, 基準温度T25(25℃)でのサーミスタの抵抗値R25は10kΩです。サーミスタ抵抗値Rと温度Tの関係式は下記のものですが、この関係式の温度は絶対温度(K)です。


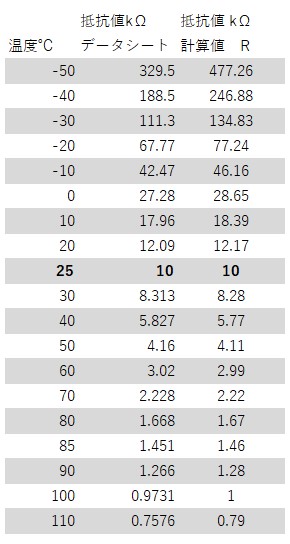
温度と抵抗値は自然対数の関数となっており、グラフを対数表で表すと温度上昇につれなだらかに抵抗値が減少しているのがわかります。データシートにある抵抗値と上記の計算式による値はほぼ一致しているのが確認できます。


温度をマイコンで計測するにはサーミスタの抵抗値を知る必要があります。抵抗値を知るには電圧に変換したアナログ値をマイコンで読み取り、マイコンプログラム内で抵抗値に変換します。

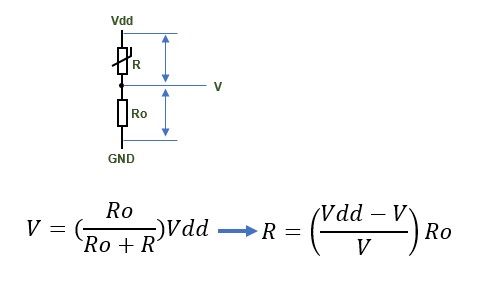
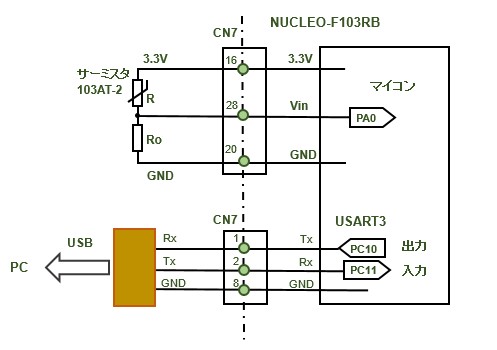
このサンプルでは上限電圧としてのマイコン電圧Vdd(3.3V)とGND間にサーミスタRと抵抗器Ro(サーミスタのR25と同じ程度の値のもの 10kΩ )を直列に接続しています。中間の電圧Vが温度変化に応じて変化しますのでこの電圧をAD変換で読み取り、下記の式で抵抗値に変換します。

サーミスタの抵抗値がわかればあとは温度に変換する式に入力して演算すればよいわけですが、この式では自然対数を使った算術演算をしなければなりません。非線形な演算のため、通常の整数での演算ではなく浮動小数点型変数を使用したものとなります。
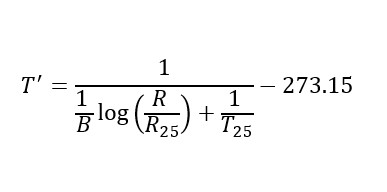

この演算を実現するには、まず自然対数log関数を使用するために"math.h"をインクルードしておく必要があります。次に温度を浮動小数点型変数で演算してください。得られた演算値をシリアル通信でモニターに送り 小数点表示させるのですが、あとはマイコン特有の注意点はなく、プログラミングの問題です。 サーミスタ抵抗-温度関係式 では絶対温度ですので、273.15を引いて摂氏(セルシウス温度)に換算します。
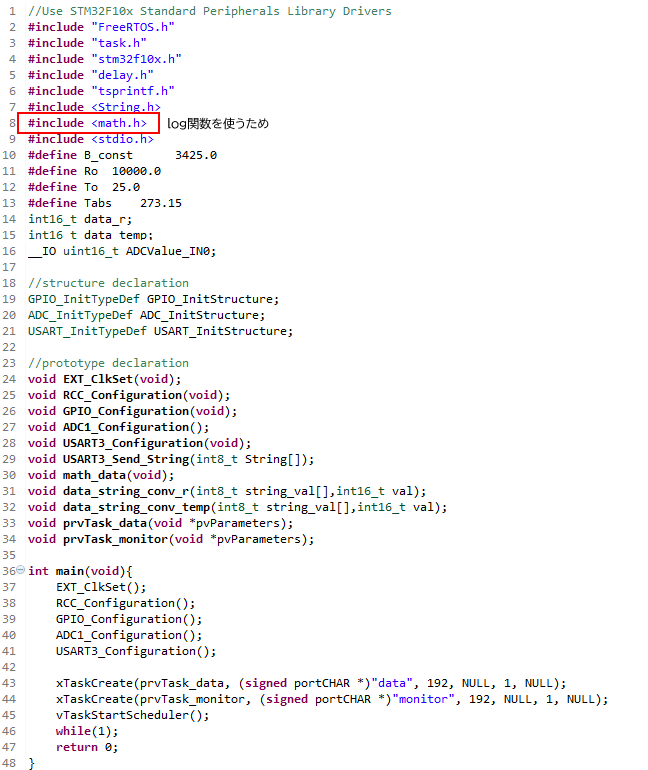

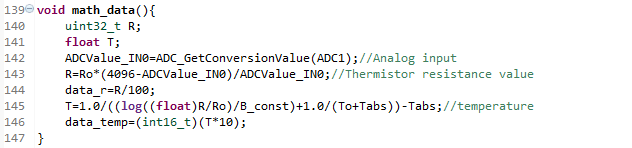
抵抗値に相当する電圧(ADCValue_IN0)をAD変換で取り込むのですがこのサンプルプログラムでは連続変換に指定していますので任意のタイミングで取得でき、141行で抵抗値に変換しています。3.3V入力時にデジタル値4096となるようにしています。142行は表示数字桁数を設定するものです。

143行でlog関数による浮動小数点演算を実施して温度を求めています。144行は表示数字桁数の設定です。


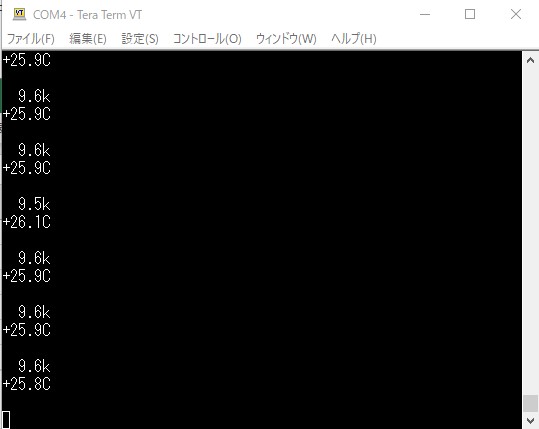
0.5秒周期でサーミスタ抵抗値と温度を表示しています。サーミスタ温度-抵抗値特性表の値とほぼ一致していることが確認できます。指でサーミスタをつまむと温度が体温近くまで上昇するのがわかります。

このサンプルプログラムは簡易的なものですが、STM32F103RB搭載Cortex-M3コアで浮動小数点演算を使った例を扱いました。他に、非線形演算のSIN関数、COS関数などをつかったアプリにも応用できます。
NUCLEO-F103RBに搭載しているSTM32F103RBはCortex-M3コアマイコンで浮動小数点を演算するためのハードウェアDSP(Digital Signal Processor)は搭載しておらず演算はソフトウェアによるものですが、それを特別に意識しないでも実現できます。このサンプルの温度演算のような比較的低速なアプリケーションでは問題はないでしょうが、例えばFFTアナライザーなど高速演算を必要とする浮動小数点演算を行うアプリケーションの場合にはハードウェアのDSPを搭載したCortex-M4など上位マイコンが有利です。



