マイコンで実現するフィードバック制御のための基礎知識【解析編】
マイコンで実現するフィードバック制御のための基礎知識【準備編 】ではフィードバック制御の概要およびモデリングした制御対象を複素数s空間にラプラス変換して伝達関数を作成するところまでをまとめています。
この【解析編】ではブロック線図の見方および伝達関数の基本形である1次遅れおよび2次遅れ系の特性を解説してから、いよいよフィードバック制御システムを設計するための勘所をできるだけ数式と物理的な観点を合わせて解説していきたいとおもいます。
特に安定性や追従性を解説するには最低限の数式で表現しなければ説明できないところもありますが、難解なものではなく感覚的に理解できるように解説しています。
目次
伝達関数とブロック線図(直列、並列、フィードバック)

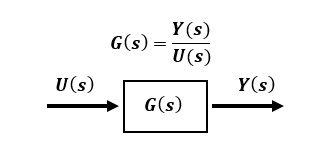
伝達関数とはシステムへの入力を出力に変換する機能を複素関数で表現したものです。時間空間の入力u(t),出力y(t)のシステムをラプラス変換した複素数空間ではそれぞれU(s),Y(s)で表すとすると、伝達関数G(s)は以下のように表現します。

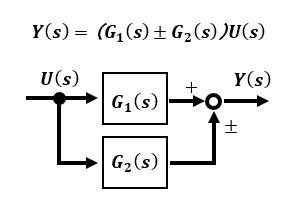
ブロック線図とは入力から出力間の伝達関数を通る信号伝達の様子がフローチャートのように機能ごとに分類されて視覚的に分かりやすく表現したものです。基本的な要素の3通りを知っておけばよいです。
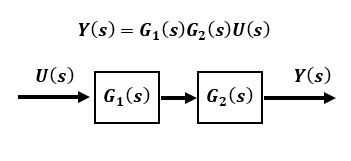
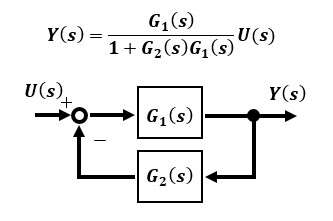
伝達関数とその特性
特にモーションコントロールにおいてはシステムの特性は伝達関数の基本形である1次遅れと2次遅れの組み合わせで表現できますので 最低限、1次遅れと2次遅れの特性を押さえてほしいと思います。他の特性は必要に応じてからでよいのではないでしょうか。
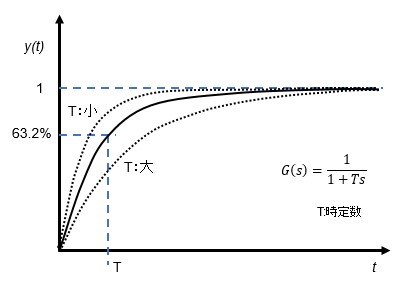
1次遅れ特性

1次遅れ伝達関数G(s)にt=0でu(t)=1のステップ入力を与えた時の出力y(t)の時間変化を見ると入力に対してある時間(時定数T)だけ指数関数特性で遅れる性質のものです。入力に対して出力がなまりますが振動は発生しません。電気回路で抵抗器RとコンデンサCで構成したRCフィルターが1次遅れ特性を持っているローパスフィルターと呼ばれるものでRとCのパラメータで時定数Tを調整できます。
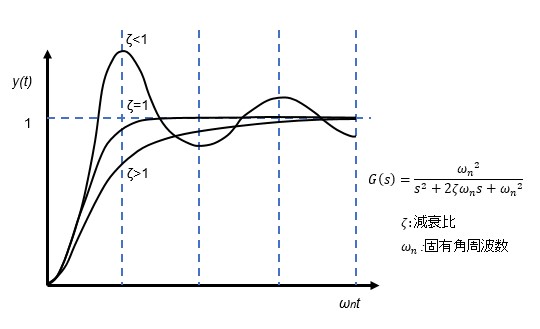
2次遅れ特性

2次遅れ伝達関数G(s)にt=0でu(t)=1のステップ入力を与えた時の 出力y(t)の 時間変化を見ると入力に対して減衰比ζに応じて応答が振動的になったり非振動的になったりしています。1次遅れ系に比べて出力信号の立ち上がり部分が滑らかなS字カーブとなっているのも特徴です。

減衰比0<ζ<1で振動的になり0に近づくほど振動が大きくなりζ=0ではついに持続振動系となって収束しなくなります。ζが1より大きい場合は非振動系となって値が大きいほど収束しにくくなります。経験的にサーボ機構などの追従制御の場合はζ=0.6~0.8、プロセス制御など定値制御の場合にはζ=0.2~0.4あたりが適当だといわれています。固有角周波数ωnは速応性の尺度で大きい値ほど振動周期が小さくなり応答性はよくなります。
物理的考察

ここで、1次遅れ系と2次遅れ系の制御対象であるものについて物理的な意味を考察してみましょう。

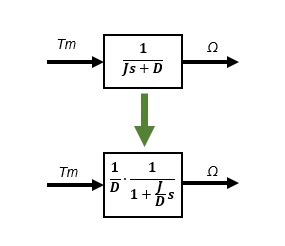
以前、DCモータの機械系をモデリングしたのでこれを例にとって考えてみます。入力がモータトルクTm、出力がモータ回転速度Ωとすると粘性摩擦Dがある条件では回転速度はモータトルクの1次遅れとなっています。

つまり、回転体にトルクを与えると、回転速度は1次遅れで動作するのです。静止したフリーの回転体にある時点で一定のトルクTmを与えると(ステップ入力)、回転体は静止状態(速度0)から回りはじめ、トルクTmが粘性摩擦Dによるブレーキ力とつりあったところで一定の回転を保ち続けます。

この入力に対して慣性Jと粘性摩擦Dにより遅れながら起動するのが1次遅れ系の物理的なイメージです。慣性Jが大きくなると時定数が大きくなり起動は鈍くなります。粘性摩擦Dが大きくなると時定数は小さくなりますが、ブレーキ力が大きくなるため出力の回転速度Ωは小さくなります。

次に2次遅れ系を考察します。回転体の回転位置(回転角度)は速度の時間積分ですのでトルクTmから見ると2次系の伝達関数となるのですが、安定している1次遅れ系を積分しただけのものですから2次遅れの振動系ではありません。
力学的な2次遅れ系の典型的なものとしては水平面上で質量mがばねkとダンパc を介して壁に接続しているモデルです。入力f(t)を加えた時の変位をx(t)とすると
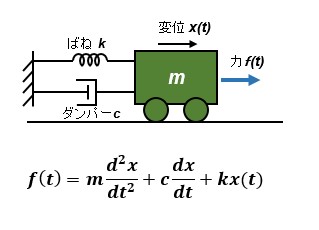
となるのでラプラス変換をすると、出力の変位は
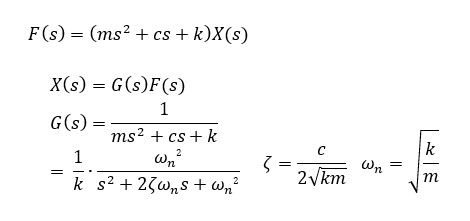
の伝達関数特性となる典型的な2次遅れ系になります。

減衰比 ζ はダンパcに比例し、質量mおよびばねk に反比例しています。ばね定数kが大きくなると減衰比ζは0に近づき振動系になり制振要素のダンパcが大きくなるにつれてζも大きくなり振動もおさまります。入力に対して振動気味で起動するのが2次遅れ系の物理的なイメージです。 ダンパcがない場合は減衰のない持続振動になります。
伝達関数とボード線図

電気回路を含めたメカトロニクスの設計では周波数特性を意識して行うことが求められます。周波数特性をグラフ化したものがボード線図と呼ばれるものです。

伝達関数は周波数領域の複素数s(=jω)の関数ですので入出力間の周波数特性として横軸を周波数成分のグラフであるボード線図をよく使用します。ボード線図には二種類あり、縦軸がゲイン(dB)のゲイン特性と、位相(°)の位相特性です。
ゲインdBとは:
ゲインdBは時間空間での正弦波入力の振幅に対する出力の振幅の比率のことで次式により定義されたものです。
ゲインdB = 20log10振幅比率 :ゲインの定義
これより、時間空間関数での振幅比率は
振幅比率 = 10ゲインdB/20
となるので0dBの時の振幅比率は1となり、入力の振幅に対して出力は同じです。20dBでは振幅比率は10倍、-20dBでは0.1倍となります。
decとは:
横軸も周波数領域の対数表記となっています。decはdecadeのことで対数スケールを表す単位です。

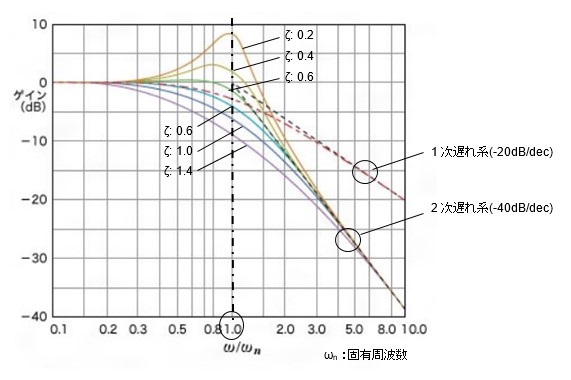
時定数Tの1次遅れ系と2次遅れ系のボード線図の見方を解説します。

1次遅れ系のゲイン特性は固有周波数ωnまではゲイン0dBつまり、振幅比率は1倍で出力は入力と同じなのですが、固有周波数を境に-20dB/decでゲインが下がっていきます。つまりこの周波数から積分と同じ特性になります。この境の周波数をカットオフ周波数f (=ωn/2π)といい、時定数Tの逆数です。カットオフ周波数以上の信号はカットし、低周波数領域のみの信号を通すことからローパスフィルターの特性を持っています。

2次遅れ系のゲイン特性は固有周波数ωnで一度ゲインが最大になるポイントがありますが、ここが振動系の共振点です。固有周波数を境に-40dB/decでゲインが下がっていきます。減衰比ζが大きくなるにつれて共振点であるゲインのピークが下がり、しまいには単なるローパスフィルターになります。1次遅れ系と異なる点は同じローパスフィルターでもゲイン降下の傾きが急であることです。これはフィルターとしてはより性能が良いことになります。フィルターの伝達関数では次数が大きいものほどこの傾きも大きくなるのでより性能が高くなります。

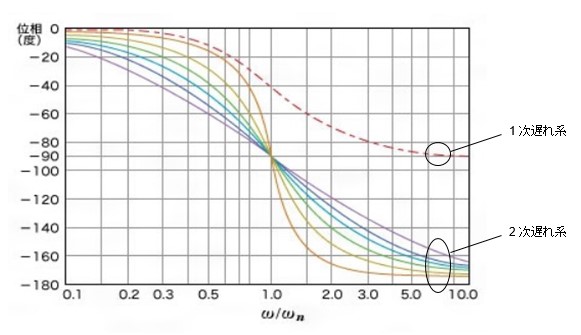
1次遅れ系の位相特性では周波数が高くなるにつれて遅れていき、固有周波数付近で45°、無限大の周波数で90°に近づいていくことを表しています。

2次遅れ系の位相特性では1次遅れ系に比べて遅れる度合いが大きく、固有周波数付近で90°、無限大の周波数で180°に近づいていくことを表しています。
伝達関数のパラメータなどを入力すると、ボード線図を描いてくれる便利なツールがインターネットで利用できますので試してみてください。
伝達関数と制御システムの安定性

これから制御の本質である安定性について解説していきます。いわゆる安定しているもとのはどういったもので、どのようなものが不安定であるかを伝達関数の式から意味を考えてみることにします。

実際に多くの計算をするためのもののではなく、理解するうえで多少数式はでてきますが、物理的な現象が数式上ではどうなるかを把握するうえでもここは避けて通ることはできない大事な部分です。
特性多項式の解(極と零点)と安定性のかかわり
一般に入力と出力の間にあるs関数である伝達関数G(s)は
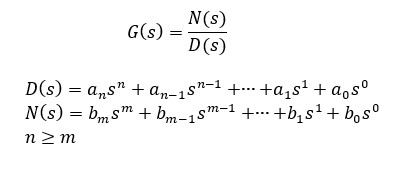
の多項式なる有利関数で表されます。

分母D(s)=0を特性多項式とよび、この解(特性根)を極と呼びます。対して、分子N(s)=0の解を零点と呼びます。システムが成り立つ必要条件として分母式の次数が分子式の次数と同じか大きいこと(n≧m)です。
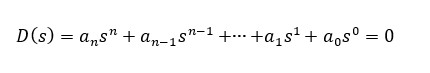

システムの安定性は主に特性方程式の極の位置によります。「主に」と書いたわけは零点もシステムの安定性に影響するわけですが、これを説明するには少し数学的で感覚的につかみにくいために最後にポイントだけまとめておくことにします。
安定性の条件(最重要):
- 極がすべて負の実数であるか負の実数を含む複素数であるとシステムは収束し安定します。
- 極が虚軸上つまり実数部=0の時は安定限界地点で持続振動します。
- 極の1つでも正の実数を含むものがあるとそのシステムは発散します。
伝達関数の分母式の次数nが分子式の次数mと同じか大きいことは自然界で存在する物理システムの必要条件なのです。mがnより大きくなることは伝達関数に微分項が含まれることになりますが、厳密な微分というものは今後の変化のことで定義より未来の情報を含んでいるために単独では自然界に存在しません。別の見方によると微分器sを時間関数に逆ラプラス変換したものは存在しないということです。ちなみに、微分の逆の積分は過去の累積です。専門的になりますが、n≧mであるシステムをプロパーといい、n>mのシステムを厳密にプロパーであるといいます。

時間関数の速度v(t)から距離x(t)はプロパーな積分で求められますが、任意の予測できない時間関数距離x(t)から厳密な速度v(t)は非プロパーな微分では求められません。主に車速メータなどで見られる速度はパルスカウントする方式で過去から現在までの位置情報を使った差分やローパスフィルターを追加したプロパーな不完全微分などにより得られたものです。
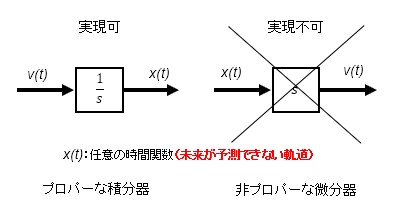

ちなみに、出力が回転速度に比例した電圧等のアナログ式タコジェネレータで計測したものは、厳密な速度と言えます。パルスカウントするディジタル式の速度計はすべて近似速度です。
収束と発散

なぜ極の実数部が負であると安定するかを説明します。
特性方程式の解(特性根) a1, a2, a3をもったシステムの伝達関数G(s)は
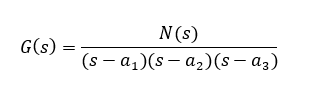
で表されます。
これを部分展開してから逆ラプラス変換をして時間関数に直すと
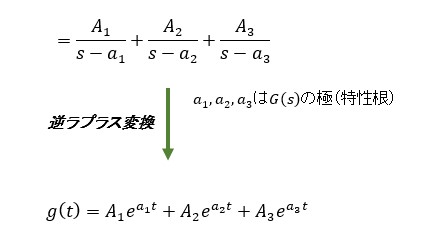
と表されます。t→∞の時、この時間関数g(t)の項が一つでも発散するとシステムは不安定になります。 そこで、g(t)が時間の経過とともに安定である条件はグラフより
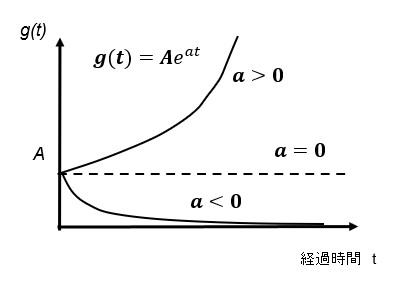
a<0つまり、 すべての極で実数部が負であることが安定化の必要条件となります。極は複素数であってもよく実数部の絶対値が大きいほど収束は速く、虚数部があると減衰振動系になります。
特性根 a に実数が含まれず虚数の共役根である場合は マイコンで実現するフィードバック制御のための基礎知識【準備編 】 のラプラス変換表1のsin関数またはcos関数に相当するので収束も発散もしない持続振動となります。
a=0の時、時間関数g(t)は定数となりその伝達関数はステップ入力に対して出力が線形に増加する積分器になります(インパルス入力に対して出力は一定)。インパルス応答とその伝達関数の物理的解釈に詳細を解説しています。
従来、制御理論においてシステムの安定性を求める方法はさまざまなものが考案されてきましたが、今では高次の特性多項式を簡単に解くツールがあり特性根は簡単に求まるので、実践では大いに利用すればよいでしょう。難解な理論をあえて理解しないでも肝心なことはできてしまいますので本質のところだけ理解しておいて大丈夫です。
伝達関数の特性根(特性方程式の解a=α+jβ)についてのまとめ:
aの虚数部βが0の場合(実数)
■ aの実数部α>0:発散
■ aの実数部α<0:収束
aの虚数部βが0でない場合(複素数)
■ aの実数部α>0:発散
■ aの実数部α=0:持続振動
■ aの実数部α<0:減衰振動
特性根の実数部が負で収束(負数の絶対値が大きいほど速く収束)、虚数部が存在すると振動系
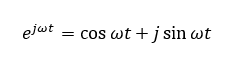
特性根に虚数が含まれると振動するようになります。これはオイラーの公式に関連しています。証明はちょっと数学的で難しいですが興味がある人は掘り下げて調べてみてください。
システム伝達関数の零点について

システムの安定性は主に特性多項式の極の位置により決まるのですが、零点が存在するときは無視できない場合があります。一般的に零点のないシステムに比べ零点の存在するシステムは応答が悪化する場合がありますので検証はすべきでしょう。

単体の物理要素では零点はあまり見られませんがフィードバックなどで結合すると出てくる場合があります。

零点は極との位置関係により出力に影響するのですが、端的にまとめると零点も極と同じく、実数部が負であることが条件です。正であるのは不安定零点と呼ばれ入力に対して逆ぶれなどの悪影響を及ぼします。零点は極に近いほど互いに相殺し合うため影響が小さくなります。また、極から負側へ十分はなれているとあまり影響は受けないのですが、極より原点に近いとオーバーシュート気味であまりよくない性質のものと頭の片隅に入れておいてください。零点における情報はあまり出回っていないのですが、こちらのサイトで詳細を解説しています。
フィードバックによる特性の改善

伝達関数の扱いになれて、システムの安定性について理解できたところでいよいよフィードバック制御の本題に入ります。フィードバック制御の主な役割は、下記の2点です。
- 不安定な制御対象にフィードバックを施すことで安定化させること
- フィードバックを施すことで、追従性を向上させたり、外乱などの影響を小さくしたりすること

フィードバックにより不安定な制御対象を安定化させることができるわけですが、その逆もいえて、安定しているシステムにフィードバックを加えることで不安定になることも十分ありえます。そこで、伝達関数レベルでフィードバックを加えたシステムに補償器と呼ばれる部分を厳密に設計して最終的にシステム全体の安定性および追従性を検証するのです。
このフィードバックの概念はモーションコントロールを始めとする機器類のものだけでなく、生物学的にも適用されているもので、自身についても無意識ではあるのですが大いに関連して日々行動しています。とても奥が深くひとつの哲学的な概念として捉えていろいろな事象について当てはめて観察してみるのも面白いかもしれません。
不安定なシステムの安定化

例えば、以下の不安定な伝達関数で表されるシステムにフィードバックループを追加することで安定化させることができるようすをたどってみましょう。
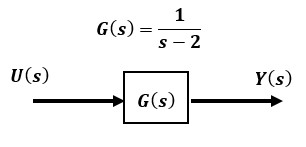
入出力間の伝達関数に正の極をもつ不安定なシステムにフィードバックを施してみます。
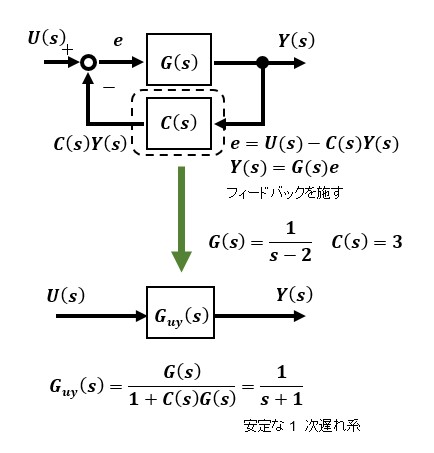

システムが安定の条件は伝達関数の極実数部が負値であることですのでこの場合は補償器C(s)を定数3として入力から出力間の伝達関数Guy(s)を算出すると、もとの伝達関数G(s)が不安定であったものが、極が負値の安定な1次遅れシステムGuy(s)に特性が改善されたことがわかります。

このようにして、フィードバックを補償器C(s)を通して施し、システムの新たな極配置をし直すことでシステムを改善することができます。補償器C(s)の設置する位置はフィードバックループ内でも、制御対象の直前でもよいのですが、これは制御対象によりますので、実践応用で設計する際には、実現のしやすさなどを考慮し、シミュレーションなどで結果をみながら判断するところです。
フィードバック制御の内部安定性

前節ではフィードバックを施すことで、不安定なシステムを安定化させる簡単な例で解説しました。例は数式上のもので現実ではそう単純なものではなく、実際のシステムにフィードバックループを構成すると少し複雑になります。フィードバックループを追加した閉ループシステムでは目標入力以外にシステムに加わる外乱やノイズ等の入力すべてにおいて閉ループシステムが安定しなければなりません。この指標を内部安定性といいます。
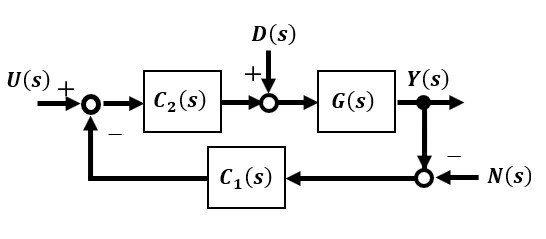

目標入力を与えたときに出力が発散せずに収束することが安定である条件ですが、目標値以外の外乱やノイズ等が入力されたときも発散しないでいることが重要だということです。

外乱やノイズを考慮しないで目標入力U(s)から出力Y(s)までの閉ループ伝達関数Guy(s)は以下のとおりになります。まず、この閉ループ伝達関数Guy(s)が安定であることが条件です。
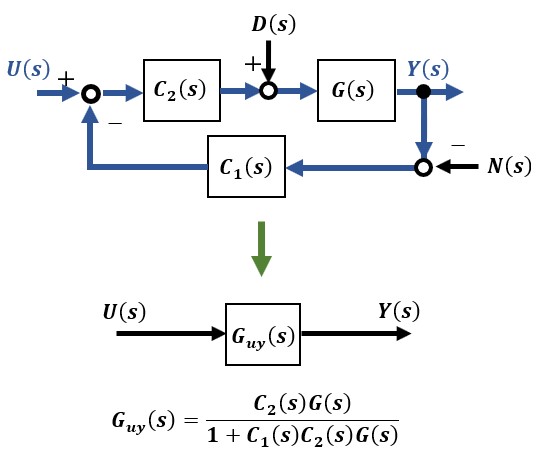

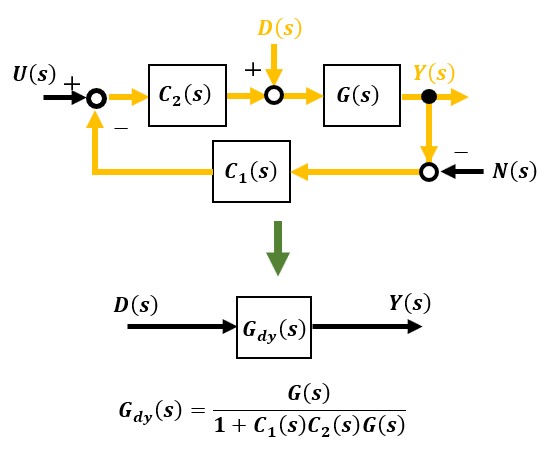
次に目標値およびノイズを考慮しない外乱D(s)から出力Y(s)までの閉ループ伝達関数Gdy(s)は以下のようになります。前節の例では補償器C2は1なのでGry(s)とGdy(s)は同じです。外乱は一般的に低周波域のものなので、Gdy(s)に周波数全域のゲインが小さい特性かハイパスフィルタの特性を持たせるのが好ましいです。

最後に、ノイズ入力N(s)から出力Y(s)までの閉ループ伝達関数Gny(s)は以下のとおりです。前節の例ではGny(s)=-3/(s+1)となりこの場合は安定していますが、補償器C1(s)=3によりノイズがゲイン倍に増幅されることを意味しています。ただし、ノイズは一般的に高周波域のものなのでこの例では時定数の大きいローパスフィルター特性をもつGny(s)を通すことになりノイズの高周波成分はカットされ出力への影響はあまりありません。
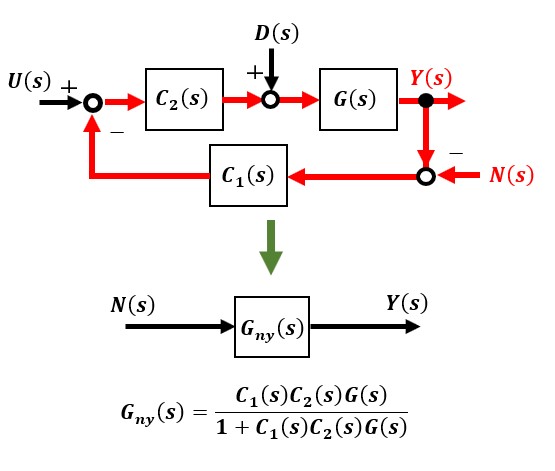
外乱抑制特性とノイズ抑制特性は概して相反する性質を持つことが多く、これを解決する理論にかなり数学的に難解ではありますがH∞制御と呼ばれるものがあります。

内部安定性の判別方法は数種類あり、例えば学問的には制御工学の教科書等でよく見かけるナイキストの安定判別法などがありますが、現実的には閉ループ伝達関数の特性根が安定なもの(上例では1+C1(s)C2(s)G(s)=0の特性根が安定)であればよいと判別できることが多いです。
内部安定性は学問としては重要な指標ですが、DCモータを使用したモーションコントロールにおいてはもともと安定したモータの特性を改善するものですので、経験上、新規の制御方式を採用したりよほど複雑な補償器を付加しない限り内部安定性についてはあまり意識することはありません。
追従性の向上

フィードバック制御のもう一つの役割に追従性があります。制御対象出力は目標値への追従が求められます。今回も、数式上の観念的な説明ではありますが、考え方の基本ですのでしっかり理解しておくと実践での応用で迷ったときに物理的なものを数式的なもので考えられるようになります。

迷ったときに感覚的でなく論理的に解析できるので地に足がついた状態でものごとを捉えることができるようになるでしょう。

今回はより汎用的に解析するために、制御対象G(s)に対して、補償器C1(s)とC2(s)をつけたもので行います。 入力U(s)から出力Y(s)までの伝達関数Guy(s)は安定であることが条件です。
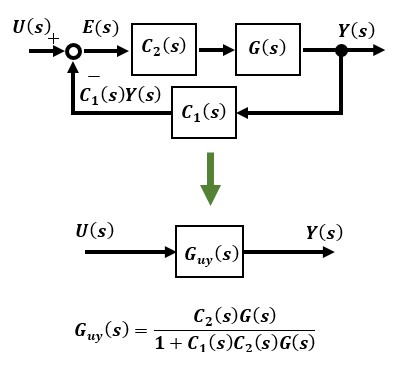

ここで入力U(s)とフィードバック量C1(s)Y(s)の差E(s)を偏差と呼び、E(s)からループにより戻ってくるまでを一巡伝達関数G0(s)とすると入力から偏差までの伝達関数は次式のようになります。
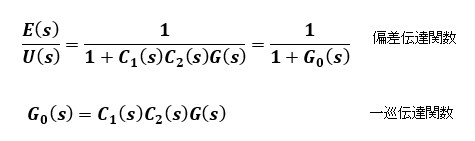

U(s)の時間関数であるu(t)に対して偏差E(s)の時間関数e(t)がt→∞のときにある値に収束すればその値のことを定常偏差とよびます。この定常偏差を入力に対してできるだけ安定して零に近づけることがフィードバック制御で追従性を向上させるための目的です。このために補償器C1(s), C2(s) を解析しながら最適なものに設計するわけです。

実際のシステムではこのような単純な形ではない場合がほとんどですが、基本的な概念はみな同じです。また、入力も、単純なステップ入力だけでなく、時間で変動する入力もありそれに追従させることをサーボ追従といったりします。

ここで、システムにステップ入力とランプ入力を与えたときの定常偏差について調べてみましょう。
定常偏差を解析するのに、最終値定理というものがあって
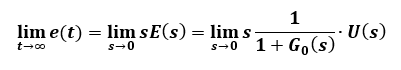
と表されます。これだけは覚えておいてもよいでしょう。

ここで入力U(s)に対する定常偏差を調べてみましょう。
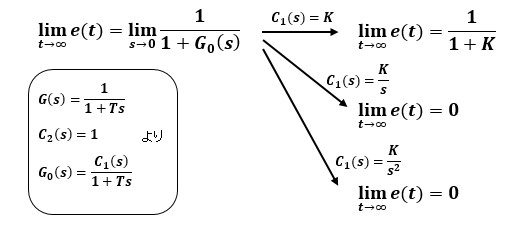
G(s)=1/(1+Ts)の安定した1次遅れ系にフィードバックしてステップ入力とランプ入力を与えた時の定常偏差をそれぞれ調べてみます。簡略化のためC2(s)=1にしています。
ステップ入力U(s)=1/sの時:
補償器C1(s)が定数Kの時は定常偏差がのこりますが、積分器を一段K/sおよび二段K/s2いれた場合では偏差は零になることがわかります。
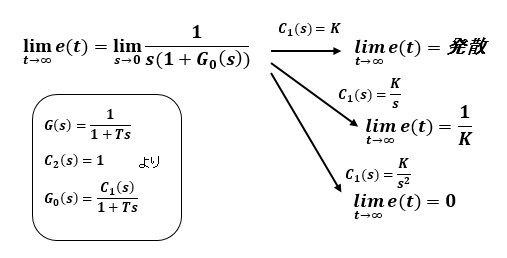
ランプ入力U(s)=1/s2,の時:
補償器C1(s)が定数Kの時は発散してしまいますが、積分器を一段いれたK/sでは定常偏差は残りますが収束します。二段いれたK/s2では零になることわかります。

以上の解析より安定しているシステムという条件付きですが、フィードバック補償器を適切に設定することで、システムの定常偏差が零になることがわかりました。

もともとある程度安定している1次遅れ系のシステムではフィードバックを施して補償器に積分器を一つ入れるだけで理論上ではありますが定常偏差をなくせるので出力を目標値に追従させることができるようになるわけです。

実際には、出力を変動させるさまざまな外乱などが存在しますので、そう単純ではないのですが、ちょっとしたシステムにはこの簡易なフィードバックでも大いに威力を発揮します。
制御理論については書籍やインターネットなどで数多くの解説がされていますが、どちらかといえば、大学の講義ででてくるような観念的なものが多いです。わかった人からみればある程度は理解できるのですが、それでも数式中心の解説になるために、すべてを理解するのは大変ですし、あまり面白み味もありません。また、制御理論には実用的でなく学術的な内容もかなり含まれているのですが初心者には本当に大事なものとそうでないものの判別をするのは難しいでしょう。
そこで、「マイコンで実現するフィードバック制御のための基礎知識」の【準備編】と本編【解析編】では大事なところのみを抜粋して解説していますので、理解して慣れた頃には次回の【応用編】も難しくはなくなると思います。
実際には理論の世界のものを実際に応用させる勘所がわかれば、とても面白いものになってきます。次回は、PID制御など実際の現場で使用されているものを紹介してからフィードバック制御を実践で応用させるための勘所を紹介するために、DCモータの例を使って解説していますので、ぜひ御覧ください。




